
Problem 1

Answer: E
Solution:
0.4+0.02+0.006=0.426

Answer: B
Solution:
2/15=8/100=0.08
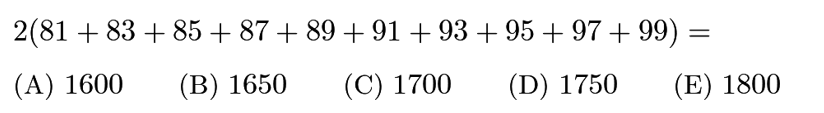
Answer: E
Solution:
Find that(81+83+85+…+99)=5*180 which gives us 2*(5*180)=10*180=1800.
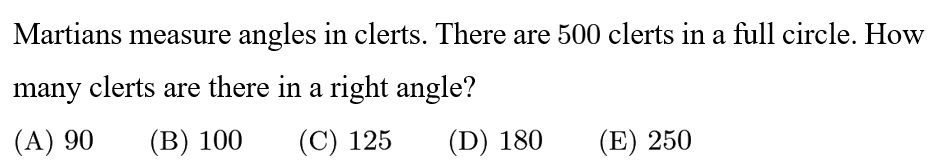
Answer: C
Solution:
The right angle is 1/4 of the circle, hence it contains 500/4=125.
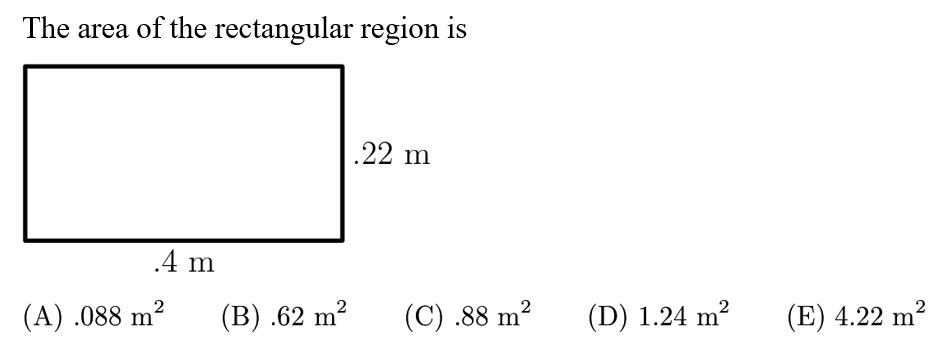
Answer: A
Solution:
0.4*0.22=0.088

Answer: B
Solution:
To get the smallest possible product, we want to multiply the smallest negative number by the largest positive number. These are -7 and 3, respectively, and their product is -21.
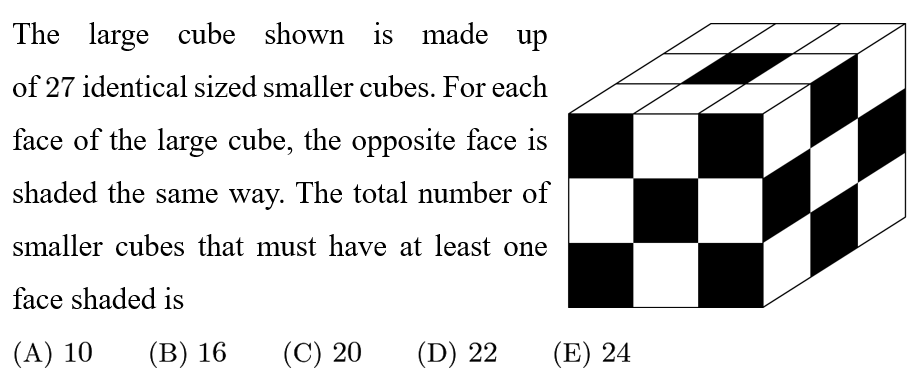
Answer: C
Solution:
Clearly no cube has more than one face painted. Therefore, the number of cubes with at least one face painted is equal to the number of painted unit squares. There are 10 painted unit squares on the half of the cube shown, so there are 10*2=20 cubes with at least one face painted.

Answer: B
Solution:
The minimum possible value of this sum is when A=B=1, which is 9876+132+11=10019.
The largest possible value of the sum is when A=B=9, making the sum9876+932+91=10899.
Since all the possible sums are between 10019 and 10899, they must have 5 digits.
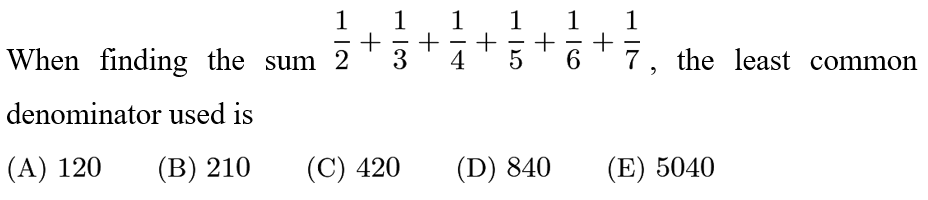
Answer: C
Solution:
We want the LCM of2,3,4,5,6,7, which is 420.
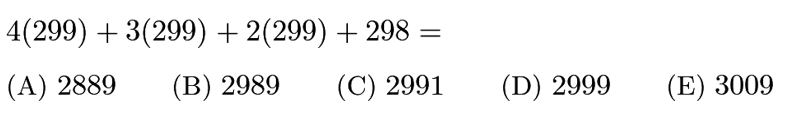
Answer: B
Solution:
=4*299+3*299+2*200+1*299-1=299*(4+3+2+1)-1=299*10-1=2990-1=2989.
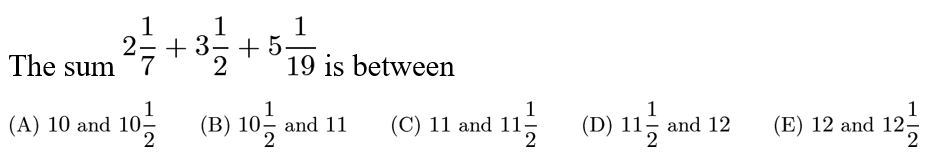
Answer: B
Solution:
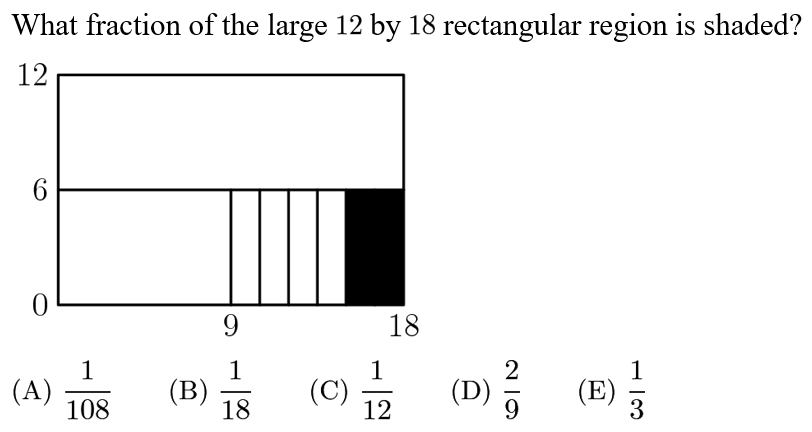
Answer: C
Solution:
The shaded region makes up 1/3 of the quarter rectangle. The quarter rectangle is then 1/4 of the large rectangle, so the shaded region takes up 1/3 *1/4=1/12 of the large rectangle.
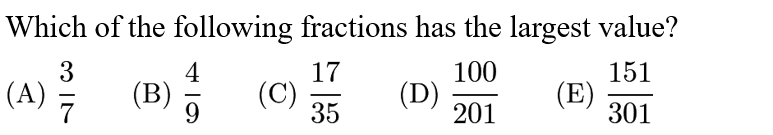
Answer: E
Solution:
Note that the first four choices are a little less than 1/2, but the last choice is just above 1/2. Thus, the largest fraction is clearly E.

Answer: B
Solution:
10,000*3600=36,000,000
Answer: D
Solution:
Let the regular price of one tire be x. then 3x+3=240, so, x=79.

Answer: E
Solution:
After the fourth game, she took 40 shots, 50% of which she made, so she made 40*50%=20 shots. Twelve of them were made in the first three games, so in the last game she made 20-12=8 shots.

Answer: D
Solution:
We know that Carl does not sit next to Bret, so he must sit in seat #1. Since Abby is not between Bret and Carl, she must sit in seat #4. Finally, Dana has to take the last seat available, which is #2.

Answer: C
Solution:
Let the original number of people in the room be x. Half of them left, so x/2 of them are left in the room. After that, one third of this group is dancing, so x/2 * (1-1/3)=x/3 people are not dancing. This is given to be 12, so x/3=12 =>x=36.

Answer: A
Solution:
2*2=4; 4*4=16; 16*16=256; 256*256>500; Clearly we need to press the button times.

Answer: A
Solution:
To show this statement to be false, we need a non-prime value of n such that n-2 is prime. Since 13 and 23 are prime, they won't prove anything relating to the truth of the statement.
Now we just check the statement for n=9,12,16, If n=12 or n=16, then n-2 is 10 or 14, which aren't prime. However, n=9 makes n-2=7, which is prime, so n=9 proves the statement false.

Answer: C
Solution:
We can just test all of these statements: 3* + 6* =1/3+1/6<>1/9; 6* -4*=1/6-1/4 <>1/2;
2* * 6*=1/2 * 1/6=1/12 = 12*; 10* / 2* =1/10 / 1/2= 1/5 =5* . The last two statements are true and the first two aren't.
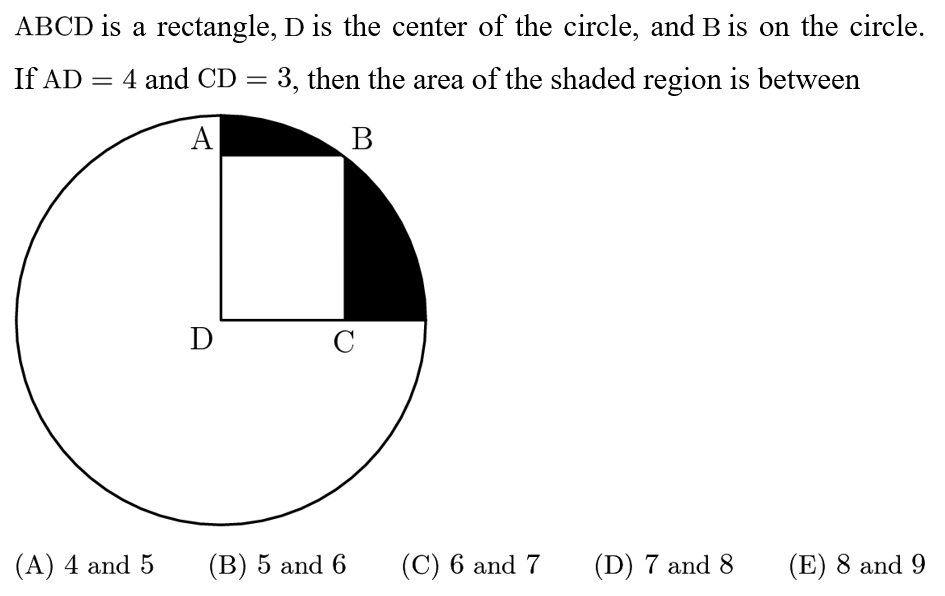
Answer: D
Solution:
The area of the shaded region is equal to the area of the quarter circle with the area of the rectangle taken away. The area of the rectangle is 4*3=12, so we just need the quarter circle.
Applying the Pythagorean theorem to triangle BCD, BD=5. Clearly is a radius of the circle, so the area of the whole circle is 5*5*Pi and the area of the quarter circle is 25Pi/4. Finally the shaded region is 25Pi/4-12=7.6.

Answer: D
Solution:

Answer: D
Solution:
Let c be the number of questions correct, w be the number of questions wrong, and b be the number of questions left blank. We are given that c+w+b=20; 5c-2w=48.
Thus, we get 7c+2b=88. Since we want to maximize the value of c, we try to find the largest multiple of 7 less than 88. This is 12, so let c=12. Then we have 7*12+2b=88 =>b=2. Finally, we have w=20-12-2=6. We wang c, the answer is 12.

Answer: A
Solution:
For the sum of the two numbers removed to be even, they must be of the same parity. There are five even values and five odd values.
No matter what Jack chooses, the number of numbers with the same parity is four. There are nine numbers total, so the probability Jill chooses a number with the same parity as Jack's is 4/9.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,